An Introduction to the Microscopical Study of Diatoms
Editors’ Note: The article below was published in 2008. In 2013, Hooke College of Applied Sciences received permission to allow the entire book to be downloaded as a PDF.
________________________
Editors’ Note: Many readers will recognize the name of Robert B. “Mac” McLaughlin as the author of a regular Diatom column published in The Microscope during the 1980’s and 1990’s. He also wrote two books in the Microscope Series on Accessories and Contrast Methods. He is a contributor to the diatom literature, and, indeed, has had a diatom named for him, Gomphonema maclaughlinii (Reichert). Over 50 years ago, while still up in Alaska and prior to his work on the diatoms of the Kenai Deposit, Mac started to write a diatom textbook for himself, acting more as a compiler or organizer of material from, generally, older, scarcer diatom works. He was, in his words, like a fish out of water, and wished to self-educate himself to be able to do meaningful work with the microscope and diatoms. He read and studied extensively, initially for his own amusement and edification, and succeeded to a remarkable degree. Then, one day, thinking that he might help others by letting them know what he had learned were the important things to study, where to find information and publications, and, in short, distill his hard-won knowledge, he started “the book”. For illustrations he wanted to use figures from Friedrich Hustedt’s publication, Vom Sammeln und präparien der Kieselalgen sowie angaben uber Untersuchungs-und Kulturmethoden-aberholden, (ABB.XI T.4, S.I., 1929); Cramer had told him that the work was long out-of-print, and that there would be no problem about using illustrations from it. Mac’s book eventually came to be over 525 typed papers, while still needing some appendices, index, table of contents, revision, and editing.
More than 25 years ago, a publisher told Mac that they wanted to prepare his book for distribution, but, incredulously, they made no progress over a ten year period! Mac was, understandably, disheartened by the whole venture, and the book was put away; in addition, he had moved to Santa Fe. Recently, the matter of the book was brought up at Hooke College of Applied Sciences, Westmont, IL and it was decided that it would be a valuable contribution to make this knowledge available online for those wishing to start the microscopical study of diatoms. As it turns out, Mac is now an octogenarian and “a dinosaur”; his eyesight is poor, and reading is a chore. He has donated his equipment, samples, and references to the California Academy of Sciences to be with the donations from Hanna. Being thus unable to do anything more with book, he has given permission to the Hooke College of Applied Sciences to do with it as they saw fit. After much discussion, it has been decided to abandon search for an editor or anybody else to attempt to complete it, and to publish it online, as it is, even to include Mac’s own sketches and handwritten notes. There is precedent for this tack, as in the re-publication of Mann’s The Bullet’s Flight, with Pope’s hand-written marginalia, and Lee’s Note-Book of an Amateur Geologist.
Mac no longer has the Hustedt book he intended to use for illustrations, but readers will find adequate illustrative material in Hustedt’s three-part Die Kieselalgen or in Schmidt’s three-volume Atlas der Diatomaceen-Kunde, both of which have been reprinted.
Thus, Hooke College feels that rather than let Mac’s 525+ page book on diatoms, descend, unseen, into oblivion, it would be better to issue it as he last left it. Accordingly, the first installment follows, and succeeding portions will be posted as quickly as they can be prepared.
Chapter 1
Morphology
Diatoms are microscopic unicellular algae. Whatever the shape or size of the cell, it consists of the same basic parts; the nucleus, cytoplasm, plasma membrane, and the cell wall.
A. Structure of the Cell Wall
Emphasis in this introduction is placed on the structure of the diatom cell wall, as opposed to the living contents, for in the main interest in diatom study is directed toward the structure and microstructure of the cell wall. Classification of diatoms and their identification pertinent to many areas of
investigation is based on the structure of, and markings on the cell wall as revealed by the light microscope. It is therefore imperative that the student of diatoms possesses a good basic knowledge of that structure and the terminology associated with it.
General Structure
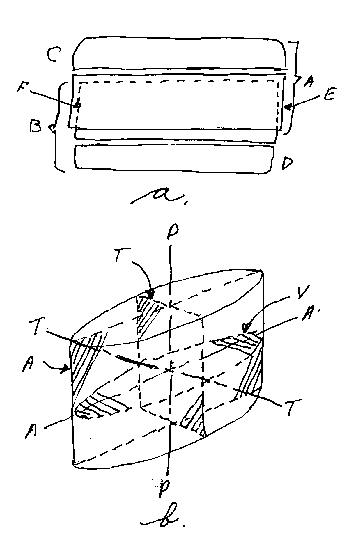
The cell wall of a diatom is composed of a siliceous material and consists basically of four distinct parts to form a box-like structure; a “top”, “bottom”, and two slip-fitting, encircling “sides”, something on the order of a pill box. The whole siliceous box, or epiderm, of a diatom is called a frustule (see Figure 1a). The components of the frustule then are the epivalve (upper valve or mantle), hypo-valve (lower valve), and two connecting bands (hypogirdle and epigirdle). One of the latter is associated with the upper valve and the other with the lower valve, the two sub-assemblies being termed the epi-theca and hypo-theca respectively. The lower valve, with its connecting hypogirdle is just slightly smaller than the upper assembly, allowing the upper epigirdle band to slip over the lower one. The two connecting bands are collectively regarded as the girdle, although occasionally they are individually referred to as girdles. Some authors also refer to the girdles as the cingula (singular cingulum). Usually a portion of the valve is bent, more or less at a 90° angle, and is called the valve mantle. It is at the edge of the valve or, more specifically, the valve mantle that the girdle band is fitted to the valve.
The entire frustule may assume many forms ranging from that of a flattened cylinder to complex and even twisted structures. The outline of a diatom is a diagnostic feature in classification and identification, and unless otherwise noted indicates an outline of a valve view of the frustule. There is a terminology associated with the outlines and shapes of diatoms. Figure 2 indicates a representative group of diatom outlines and the terms used in describing them.
B. Symmetry
The very wide variety of geometric shapes and features connected with diatom morphology results in numerous patterns. When a motif such as a particular structural feature of the valve or frustule is repeated systematically, the result is a periodic pattern. Diatom structure by its very nature then, is amenable to being referenced to some system of symmetry. Symmetry in the diatom frustule may be regarded as the correspondence in size, shape, and relative position of its parts that are on opposite sides of a dividing line or median plane, or that are distributed about a center or axis.
The symmetry of diatoms is related to an established set of axes and associated planes. Figure B illustrates the principal axes and planes to which diatom symmetry is referred. The pervalvar axis P-P joins the center points of the two valves (upper and lower). The apical axis A-A (sometimes called the sagittal axis) connects the two ends (apex; apices) of a valve such as in the genus Navicula. The transapical or transverse axis T-T lies perpendicular to the apical axis on the valve of the diatom. In circular forms the transapical and apical axes are the same length (the diameter) which is then sometimes referred to as the transvalvar axis. The apical and transapical axes determine the valve surfaces or basic symmetry planes. The apical (AA) and pervalvar (PP) axes define the apical plane (A) or the sagittal section (T). The transapical (TT) and pervalvar (PP) axes define the transapical plane or the transverse section. The apical (AA) and transapical (TT) axes define the valvar plane (V).
A.
A. Epitheca
B. Hypotheca
C. Epivalve (mantle)
D. Hypovalve
E. Epigirdle
F. Hypogirdle
B.
AA Apical axis
TT Transapical axis
PP Pervalvar axis
T Transapical plane
A Apical plane
V Valvar plane
Schematics
Axes, planes and principal
Construction features of the frustule
- Circular
- Narrow ellipticity
- Broad elliptical
- Panduriform
- Linear
- Clavate (club-like)
- Obovate
- Narrow lancolate
- Broad lancolate
- Rhomfiod
- Semi lancolate
- Arcuate
- Sigmoid lancolate
- Sigmoid oblong
- Sigmoid linear
- Rectangular
- Auricular
- Cymbiform
- Tersive
- Quadrangular
- Genuflexed
- Triangular
Terminology of Diatom Outlines

The symmetry of the various genera of diatoms differs in relationship to these three axes. How the symmetry differs is important to systematic description of the genera of diatoms.
Not only is the symmetry of the diatom frustule important to systematic description, but perhaps is even more important to the student of diatoms in forming a three-dimensional conception of various types of frustules that ordinarily are seen in the light microscope as two dimensional objects. Although by examining the frustule in a number of optical sections one can build a three-dimensional mental picture, the visual concept is considerably enhanced by other knowledge of spatial relationships of the various parts. Comparison might be drawn to the value of the knowledge of descriptive geometry and mechanical drawing to macro-objects.
For this latter reason, as well as for the former, considerable space is devoted to basic symmetrical relationships of the diatom frustule in this book. It is felt that the beginning Diatomist, or any Diatomist not familiar with these concepts, can benefit by familiarization with them. Because of the great variety of configurations of the diatom frustule and the sometimes complex relationship of its various parts, any of a number of basic symmetry systems could be formulated. Friedrich Hustedt (1929) provided an extensive system to describe diatom symmetry many years ago. I have freely translated from the German, and paraphrased and adapted much of his text and illustrations in the following material on diatom symmetry.
The definition of symmetry previously stated requires, in part at least, that there is a correspondence in size of parts on opposite sides of a symmetry plane. Since the epitheca of a diatom is larger than the hypotheca, then the so-called basic symmetry plane determined by the apical and transapical axis in reality becomes an orientation plane or plane of similarity. In the strictest sense it cannot become a plane of symmetry and the pervalvar axis could never be termed iso-polar. However, because the inherent construction of diatoms is such that the difference in size between the epitheca and hypotheca is very small we can, for practical purposes, regard the axes and planes described as adequate for diatom symmetry purposes. For that reason, and on the basis of practicality, the pervalvar axis can then be either isopolar or heteropolar.
The designation isopolar or heteropolar, with reference to any of the axes of symmetry is, in part, descriptive of diatom symmetry. For instance, the pervalvar axis of Navicula Peregrina (Figure 3A) intersects the epitheca and hypotheca of the frustule at points that are termed poles of the axis. If those points or poles intersect surfaces that are identical in structure the axis is termed isopolar. If they intersect surfaces that are not identical, as in Achnanthes brevipes (3B) for instance, the axis is termed heteropolar. For the two examples, the former determines that the pervalvar axis is isopolar and the latter is heteropolar. Similar conclusions may be drawn for the other two axes (apical and transapical) in reference to particular diatoms. In Gomphonema olivaceum (3C) the transapical axis is isopolar, whereas in Cymbella tumida (3D) it is heteropolar. In the former, although the outline is curved, the intersecting surfaces are the same. In the latter the intersections of the transapical axis are on dissimilar surfaces, one being curved much more than the other. In Surirella linearis (3E) the apical axis is isopolar, but in Rhopalodia vermicularis it is heteropolar. From this it is seen that a diatom frustule may be described in a limited way but using a polar designation for each of the three axes of symmetry.

On the basis of the symmetrical relationships of diatom structure there are two major divisions recognized:
- A group in which the pervalvar axis is isopolar (with the practical assumption mentioned previously). There are at the very least two isopolar or several heteropolar transverse axes possible which are perpendicular to the pervalvar axis. When the transverse axes are of equal length, the form is monaxial, and when they are of unequal length, they are heteroaxial (such as in bilateral diatoms). This group is termed line-symmetrical.
- The second group is plane-symmetrical. Outside of the heteropolar or isopolar pervalvar axes, there are only two transverse axes possible, of which at least one is heteropolar.
It is not possible to express the attributes of all diatom forms in terms of pure symmetry. Some frustule constructions involve twisted, or tersive, forms that complicate the symmetrical relationships. For such cases there are three main types of symmetry concepts that often suffice:
A. Mirror Symmetry. One valve is the mirror image of the other.
B. Diagonal Symmetry. One valve as compared to the other is rotated about the pervalvar axis 180°.
C. Antisymmetry. A combination of A and B above. The mirror image of one cell-half is rotated 180°.
I. Line-Symmetrical Frustules
1. Monaxial Frustules (Figure 4).
Examples of monaxial frustules are in the genera Coscinodiscus, Triceratrium and Aulacodiscus. A short analysis in each case will provide insight into the variations possible.
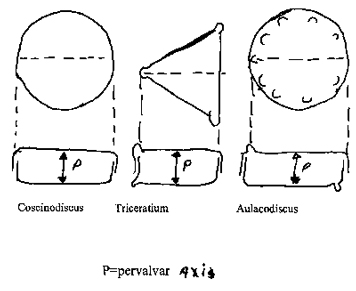
Coscinodiscus Pervalvar axis is isopolar, with an infinite number of isopolar transvalvar axes. The cell referred to the valvar plane (Figure 1B) is mirror-similar, and each of the innumerable median planes divides the frustule in two mirror symmetrical halves. All axes are straight?
Triceratrium (a three-process form). The pervalvar axis is isopolar. There are three heteropolar transverse axes from the processes to the center of the opposite side. The frustule is mirror-similar to the valvar plane, and to each of the meridian planes is mirror-symmetrical. All axes are straight.
Aulacodiscus (a form with five processes). The pervalvar axis is isopolar, and there are five isopolar transverse axes from the processes through the center to the opposite side. The frustule if diagonally-similar to the valvar plane and for each of the five median planes is mirror-symmetrical. All axes are straight.
2. Heteroaxial Frustules
Examples of this type-form are divided into two different cases. The first case is that in which the frustule is symmetrical in two planes and similar in one. Two generic types illustrate this (Figure 5).

Naviculalinearis (form with a straight raphe. Three straight isopolar axes. The frustule to the valvar plane is mirror-similar, and to the apical and transapical planes is mirror-symmetrical. The second case is that in which the frustule is symmetrical to one plane and similar in two (Figure 6). Two examples of this are:

Nitzchia sigma Three isopolar axes, of which the apical axis is not straight but S-shaped. Both other axes are straight. The frustule to the valvar plane is anti-similar, for the epitheca is a similar mirror-image of the hypotheca, but is twisted by 180°. The reason for this relationship in this species, is the curvature of the apical axis. This causes the keel to curve in a concave direction on one side and a convex direction on the other side.
Pinnularia viridis. Three straight isopolar axes. The frustule is diagonal-similar to the valvar plane and apical plane, because the raphe system on each cell-half is oppositely oriented to the other in relation to the apical axis. The frustule is mirror-symmetrical to the transapical plane.
II. Plane – Symmetrical Frustules (Figure 7).
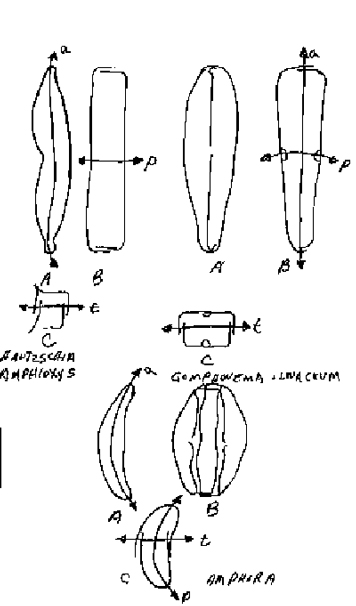
Examples of this group are found in the genera Hantzschia, Gomphonema, Amphora, Achanthes and Gomphocymbella. These include several types of symmetrical relationships.
The first case is that the frustule is to one plane symmetrical, one plane similar, and one plane asymmetrical. Three examples of this case are:
Hantzschia. Three isopolar axes. The pervalvar and transapical axes are straight, and the apical axis is curved. The frustule is mirror-similar to the valvar plane, to the transapical plane mirror-symmetrical, and to the apical plane asymmetrical. The curved apical plane divides the frustule into ventral and dorsal halves.
Gomphonema olivaceum. The pervalvar and transapical axes are isopolar, and the apical axis is heteropolar. The apical and transapical axes are straight, while the pervalvar axis is curved. The frustule is mirror-similar to the valvar plane, to the apical plane mirror-symmetric, and to the transapical plane asymmetric.
Amphora. The pervalvar and apical axes are curved and isopolar. The transapical axis is heteropolar and straight. The frustule is mirror-symmetrical to the valvar plane, the transapical plane mirror-symmetrical, and to the apical plane asymmetric.
Achnanthes inflate (Figure 8). The pervalvar axis (b) is heteropolar, and the apical (a) and transapical axis (t) isopolar. The pervalvar (P) and transapical axes (t) are straight and the apical axis (a) is undulate crooked. The frustule (A2) to the apical a valvar planes is asymmetrical, and the pseudoraphe of one valves is eccentrically displaced, while the raphe on the other valve (A1) runs with the apical plane.
The third case is when the frustule is similar to one plane and asymmetrical to two.

Gomphocymbelle (Figure 9). The pervalvar axis is isopolar, while the apical and transapical axes are heteropolar. The pervalvar and apical axes are curved and the transapical axis straight. The frustule is mirror-similar to the valvar plane (A), and to the apical (B) and transapical (B) planes is asymmetric.

Comments
add comment