Sénarmont Compensation: How to Accurately Measure Small Relative Retardations (0-1λ)
Introduction
Compensators consist of thin-sections of minerals (e.g., quartz, calcite, gypsum/selenite, mica, etc.), or polymer film equivalents, whose thickness and optical orientation are carefully controlled so as to provide known values of retardation and known direction of high and low refractive indices. When introduced into the light path of a polarizing microscope, these known retardation values and refractive index directions are superimposed on an unknown anisotropic specimen and, by noting the resultant effects (addition or subtraction of retardation, etc.), the microscopist obtains valuable identifying characteristics about the sample.
Compensators, such as the first-order red (530 nm; 550 nm; also known as the “gypsum plate,” or “selenite plate,” or “sensitive violet”), the quarter-wave plate (λ/4; ~137 nm), and the quartz wedge (3-7 orders; 1-4λ), are standard accessories used with polarizing microscopes for determining an anisotropic specimen’s optic sign (sign of double refraction), sign of elongation (location of high and low refractive indices in an elongated specimen), and characteristic birefringence. Birefringence determination requires that one obtain the sample thickness and retardation color (B = r/t 1000). For the majority of samples encountered by industrial microscopists, an estimate of the thickness obtained through use of a calibrated eyepiece micrometer, and an estimate of the retardation color obtained by reference to a Michel-Lévy Interference Color Chart (1), are usually sufficient, along with a couple of other characteristics, for rapid sample identification. For the purposes of this article, it will be assumed that the reader is generally familiar with these procedures.
Problems in obtaining the birefringence, and, therefore, the identification, arise especially when the retardation colors of the sample are very low (shades of gray in the lower part of the first order) or very high (100-200+ orders). These very low or very high retardation colors may be due to the sample being either very thick or very thin, or having very low or very high characteristic birefringence, or both.

Look at Figure 1, for example; this is a 30 µm thick rock thin-section as viewed between crossed polarizers using a 4X objective for a visual magnification of 40X. The individual mineral grains that make up this rock section are all lying at different orientations, and showing many shades of white and gray. When I view this figure filling up my monitor screen, I can go from grain to grain and name off colors: snow white, off- white, bone, ivory, cream, steel gray, bluish gray, greenish gray, light gray, medium gray, dark gray, charcoal, blue-green gray, olive gray, slate gray, gun metal, mushroom, etc. What I need, however, are not these often-creative verbal descriptions, but a value in nanometers, that the color I am looking at corresponds to; this is why I prefer a Michel-Lévy Interference Color Chart with colors printed as accurately as possible, but with the names of the colors as well. Only with an accurate determination of interference color can I obtain the characteristic birefringence that I need to identify the mineral (and, of course, the sample need not be a mineral; it could be anything). A little later, you will see from experiments I made with experienced microscopists that their estimates of retardation are not very accurate. The accurate measurement of very low or very high values of retardation is the realm of the specialized compensators. For very low values of retardation, there are the Brace and Brace-Köhler compensators which measure in the range 0-1/10λ, 0-1/20λ, and 0-1/30λ; many bio-medical specimens fall in this category. The Berek compensators are made for measuring larger ranges of retardation: 0-3λ, 0-20λ. The Ehringhaus compensators are used for measuring very large values of retardation: 170-200+λ; these are useful for highly birefringent samples, which also may be thick.
The Berek compensator is particularly well-suited for measuring retardations from zero up to many orders. It is based on an experimental compensator by W. Nikitin [Drehbarer Compensator fϋr Mikroskope. Zeitschr. f. Kryst., XLVII (1910), 378-379], in which a crystal plate (quartz in the early version made by Fuess) cut perpendicular to the c-axis is introduced above the objective. In its starting position – pointer set at “0” – the crystal surface is normal to the instrument axis, and the field of view will be dark between crossed polarizers, because the uniaxial indicatrix in this position exhibits a circular index ellipse (retardation 0). The crystal plate can be tilted about the direction of vibration of the ordinary ray, so that the circular section changes into an index ellipse in which the ratio of major to minor axis increases with the tilt angle; the effective thickness is thereby increased. As with Sénarmont compensation, the anisotropic specimen is oriented in a subtractive position so that at some tilt angle extinction occurs, provided the compensator’s range is sufficient for the sample. Berek made mechanical refinements to this compensator so that the tilt angle could be read to 1/10 of a degree (1/20 degree in the current version); and he further developed the equations and tables to convert tilt angles into retardation values. The resolution of the readout of a current Leica/Leitz 5-order Berek compensator with magnesium fluoride crystal plate is equal to 0.2nm at a retardation of 3nm; 0.5nm at a retardation of 25nm; and 2nm at a retardation of 556nm. Many microscopists find the Berek compensator more useful than the Sénarmont, provided they can justify the additional expense. The Sénarmont does have higher resolution, but it is only realized by averaging over several measurements. Over the last 170 years or so, there have been about a hundred different kinds of compensators described and made, but only the simple fixed ones and a couple of Bereks and Brace-Köhlers have been available new in the last two or three decades. You can read about many of these specialized compensators (Babinet, Bravais, Soleil, Biot, Savart, Klein, Traube, Sommerfeldt, Wright, Nikitin, Evans, Von Fedorow, Von Chrustschoff, etc.) in Johannsen’s Manual of Petrographic Methods (2).
Sénarmont Compensator
Enter the Sénarmont compensator! The Sénarmont (de Sénarmont) compensator is an example of a simple, fixed, relatively inexpensive compensator that is still available for purchase, but somehow seems to have become lost in the shuffle. Sénarmont compensation is an elegant technique that utilizes monochromatic light, together with a rotatable, graduated analyzer, for accurately determining small retardation values with the accuracy of the unit of the monochromatic light (nanometers). It is particularly good for determining those retardations in the low first-order gray region that are the most difficult to estimate accurately (<300 nm). This can also be done with most Bereks, either through tilt reading and use of the accompanying chart, or by plotting tilt versus retardation, and reading off the curve, but not nearly so cheaply. The Sénarmont compensator consists of an accurate quarter-wave plate oriented so that one of its vibration directions, usually the high index (slow direction), is parallel to the polarizer vibration direction (not at 45° as with the usual λ/4 compensator).

Figure 2 shows Sénarmont compensators made by four different microscope manufacturers; the high refractive index (Z’, γ, Ng) is indicated on each. At upper-left of Figure 2 is a Sénarmont compensator, labeled as such, made by Nikon; the high refractive index direction (Z’), low refractive index direction (X’), retardation (¼λ), and the measuring wavelength (546 nm) are all indicated directly on the compensator. Below the Nikon, in the middle, is the Olympus Sénarmont compensator, with the high refractive index direction (γ) indicated; the “U-CSE” is the Olympus catalog designation for the Sénarmont compensator; the measuring wavelength, not indicated on the compensator, but given in the Compensators Instructions, is 546.1 nm (e-line). The third, bottom, compensator on the left side is the Russian-made LOMO Sénarmont compensator, in which the Np (petite; low index) and Ng (grand; high index) convention is used; the retardation (¼λ) is indicated; the measuring wavelength is given in the operator’s manual as 551 nm. Note that, when inserted in the 45° compensator slot, the low refractive index of the LOMO Sénarmont compensator runs east-west, parallel to the polarizer vibration direction. The compensator in the lower right of Figure 2 is a Leitz quarter-wave compensator “in subparallel” position (γ, gamma, the high refractive index is perpendicular to the polarizer in this case, because the microscope, this was designed to be used with, pre-dates today’s DIN standard, and has its’ polarizer normally oriented north-south). In this compensator, the plate may be rotated through a few degrees for the exact setting of the extinction position. Note the measuring wavelength specified, 540 nm; Leitz also made one for 589 nm. The current Leica Sénarmont compensator, with geared crystal plate, specifies 546 nm.
The Nikon, Olympus, Leica, and LOMO Sénarmont compensators conform to DIN standard, and, thus, fit in compensator slots that are 6 mm X 20 mm.
The green filter in Figure 2 is a reminder that an interference filter supplying the specified measuring wavelength must be in the light path when measurements are made.
Besides the Sénarmont compensator and monochromatic light, the only other requirement for Sénarmont compensation is a rotatable, graduated analyzer; research-grade polarizing microscopes still come equipped with this feature, but simple, student-grade polarizing microscopes, with non-rotatable, in-out-only analyzers will be incapable of measuring retardation. For most microscopists in industry, this will be the first time the graduations feature of the rotatable analyzer will have been used.
Procedure for Sénarmont Compensation
Whenever I am in the midst of a Sénarmont compensation, invariably an on-looker will ask me what I am doing. When I tell them I am doing Sénarmont compensation, they say they never heard of it, and ask me where they can learn about it. I usually suggest Johannsen (2) or Weinschenk (3) or Wright (4), or some similar reference in petrographic methods, and, invariably, the eventual response is that a description of the procedure is not in those works. And it is true. Johannsen (2) provides historical background on many types of compensators; Wright (4) does not describe the procedure, but states that it only provides retardation to 3 nm, so it is unsuited to petrographic applications. Hartshorne and Stuart (5) provide an explanation of the principle of the Sénarmont compensator, but Bloss provides a detailed discussion of the theory and practice of this technique, together with outstanding illustrations, in his book on the spindle stage (6). For those unable to locate this 1981 book, or the earlier German-language texts, the procedure for Sénarmont compensation will be described here.
First of all, the microscope preparation for all quantitative compensation measurements is the same: the eyepiece with cross hair graticule should be used, because all samples will be observed at that point which lies directly under the cross. Also, for these measurements, we want a narrow beam of light, not one of high NA; the highly oblique light rays from high NA condensers travel farther through the sample than the axial rays do, leading to composite results; therefore, swing the top lens of the condenser out, and close the aperture diaphragm to obtain axial beams only. If weak light sources are used, or more resolution is needed, the aperture diaphragm will have to be opened somewhat, although measuring accuracy will decrease.
Let’s run through the steps using a synthetic fiber. I have selected, from the McCrone Microscopes and Accessories Fiber Reference Set, an acrylic fiber with round cross section.
Step 1. Place the fiber specimen on the stage, and move it until it lies under the cross hairs. Swing out the top lens of the condenser, if you have not already done this, and close the aperture diaphragm. Insert the analyzer. Rotate the stage, and observe that the fiber has parallel extinction; it “disappears” when it is lined up with either the vertical or the horizontal cross hair. (Note that, for specimens with oblique extinction, this extinction position will not necessarily occur when the fiber is parallel to a cross hair.)
Step 2. Rotate the stage 45° to bring the specimen to maximum brightness (45° from extinction), or engage the lever or knurled knob beneath the stage that activates the 45° click-stop positioner. Figure 3 illustrates this step with the acrylic fiber, using a 40X objective; the fiber displays a gray interference color, against a black background. We need the sample’s high refractive index NE/SW and, to test for this, we insert a first-order red plate. Figure 4 shows the fiber displaying an orange color. The fiber is about 100 nm gray to begin with, so that when 550 nm is superimposed with its gamma (high index) NE/SW, the results can only be additive (550 nm plus 100 nm equals 650 nm, or blue) or subtractive (550 nm minus 100 nm equals 450 nm, or orange). In this case, the color went downscale on the Michel-Lévy chart, telling us that the low index of the fiber lies parallel to the high index of the first order red plate. This fiber has a negative sign of elongation, so we rotate the stage 90°, so that the fiber is now oriented NW/SE (Figure 5), and the high refractive index (slow direction) is across the fiber width, oriented NE/SW. You cannot make a mistake with this, because if you get it wrong, you will not get extinction when the analyzer is rotated.
Step 3. Remove the first-order red plate, and insert the Sénarmont compensator into the 45° slot all the way. Place the appropriate monochromatic interference filter into the light path (in this example, I am using an Olympus Sénarmont compensator, which calls for 546.1 nm, and so I have placed an Olympus 9-B322, 45 mm diameter 546 green interference filter in the filter carrier over the light exit port). Figure 6 is now the appearance of the sample; the fiber is green, and the background is black.
Step 4. Rotate the analyzer until the part of the specimen to be measured – that lying immediately beneath the cross – becomes black, or as dark as possible; the background, which was black, will lighten as you do this (Figure 7).
Step 5. Measurement. Read the analyzer setting to within a tenth of a degree using the vernier. Two examples will illustrate how a 20-division vernier, and a 2° per division analyzer scale are read; and how a 10-division vernier, and a 1° per division analyzer scale are read.
Figure 8 is a close-up of the analyzer of an Olympus BH-2 polarizing microscope. Note that the upper rotatable scale is 180° in length, and is divided into 2° units. The lower, fixed scale is the 20-division vernier, which allows the 2° units of the upper scale to be read to 0.1°, i.e., 0.1° per division. In Figure 8, the analyzer reading is taken from the “0” of the vernier. In this example, the “0” fiducial mark of the vernier lies between the 36° and 38° marks, but decidedly closer to 36°. 37° would be exactly between 36° and 38°, but the reading is more than 36°, but not 37°. Next, look at the vernier scale marks to find the one line that exactly matches up with a line on the main scale; in this case, it is the 4th vernier division (it will be one of those between “0” and “10”). This vernier division number 4 is the decimal value (0.4°) that is added to the base reading (36°). Thus, the analyzer reading in Figure 8 is 36.4°.
Let us see how this same measurement is read with a 10-division vernier, and a 1° per division analyzer scale. Figure 9 is a close-up of the rotating, graduated analyzer on an Olympus BX-51 polarizing microscope. Here, each division on the knurled wheel that rotates the analyzer is worth 1°; the fixed vernier below has ten divisions, each worth 0.1°. To read this style of vernier, again go to the “0” of the vernier, and note that it lies somewhere between 36° and 37°. Record the lower number, 36°, and now look to see which vernier line is exactly lined up with a main scale line. In this case, it is the 4th vernier line (0.4°); therefore, the total reading is 36° + 0.4°, or 36.4°.
Once more, for practice. Figure 10 is a close-up of another analyzer setting on the Olympus BH-2. Note that this time, the “0” of the vernier lies between 22° and 24°, but closer to the 24°. Now look at all of the vernier lines, and you will see that the 12th line exactly matches up with a main scale line. Ten of the 12 vernier divisions represent 1° (0.1° per division), so the 1° is added to the base reading 22° (to equal 23°), and the remaining two of the 12 divisions represent 0.1° each, or 0.2°, which gets added to the base reading, now 23°, to obtain an analyzer reading of 23.2°.
Figure 11 is a close-up of the Olympus BX-51 analyzer, using the same example. Here, start at the vernier “0” and note that it indicates a base reading of more than 23°, but not 24°. Next, look at all of the vernier division lines, and note that it is the second line that exactly lines up with a main scale line. This second line represents 0.2°. The 0.2° is added to the base reading, 23°, for a final analyzer reading of 23.2°.
These explanations of how to read an analyzer vernier take longer than actually doing it, once you get the hang of it.
OK, back to our fiber sample.
Step 6. Calculation. Let the angle of the analyzer rotation be θ. Then the retardation, r, in nanometers, will be obtained from:
The minimum analyzer rotation is 0.1°, which, when multiplied by 3.033 yields a minimum measurable retardation of 0.3 nm, using a wavelength of 546 nm. In practice, the extinction position cannot be repeatedly set with 0.1° accuracy. With a cylindrical fiber, one has to concentrate one’s attention at the very center of the fiber. In one case, I made eight successive determinations to check reproducibility. I obtained readings of 37.3°, 37.1°, 37.1°, 37.0°, 36.7°, 35.8°, 36.9°, and 36.7°. To obtain a more accurate result, the analyzer reading is taken, as described, using the best evaluation of the extinction position. Then the specimen is rotated 90°. The analyzer will now have to be rotated to the other side of the crossed position to obtain extinction. Half the sum of the two angles is used to calculate the retardation. In the case of the above acrylic fiber, a reading of 161.0° was obtained. 180° – 161° = 19°. 18.6° + 19.0° = 37.6°.where λ is the wavelength (nm) of the monochromatic light. For any given Sénarmont compensator, the specified wavelength does not change, so that λ/180 will be a constant. With the Sénarmont compensator used in this example, the specified wavelength is 546 nm, and 546/180 = 3.033+ nm per degree. Therefore, one simply has to multiply the analyzer reading by the constant 3.033 to obtain the retardation. In the case of the acrylic fiber, the analyzer reading to obtain the extinction shown in Figure 7 was 18.6°. 18.6 X 3.033 = 56.4 nm.
37.6°/2 = 18.8°. 18.8 X 3.033 = 57.0 nm. The retardation of the fiber shown in Figure 3 is 57.0 nm.
To obtain still greater accuracy, the extinction positions need to be set using one of the half-shade methods with the Wright eyepiece, or by measuring light intensities at 32 evenly spaced analyzer angles which encompass 180° of analyzer rotation–harmonic analysis using personal computers and Jamin-Lebedeff optical systems can be used to determine analyzer position to 0.001° (7).
By the way, if 0.1° on the analyzer rotation reading represents 0.3 nm, then 45° (45 X 3.033) represents 136.5 nm; 90° (90 X 3.033) represents 273 nm; 135° (135 X 3.033) represents 409.5 nm; and 180° (180 X 3.033) represents 545.99 nm, in other words, one order. The Sénarmont compensator is good for measuring within one order; for samples showing more than one order, the quartz wedge, or other appropriate compensator, is used first to determine the number of whole orders.
Before making any of these measurements, I had taken a great deal of time in setting up my microscope, using orientation slides, natrolite fibers, and other critical test specimens, to ensure that my eyepiece cross hairs and vibration directions of both polarizer and analyzer coincided exactly. With polars fully crossed, move your specimen out of the field; there should be only blackness. Now insert the Sénarmont compensator while looking at the center of the field. Mine remained black, but you may see the field-of-view, or a part of it, lighten just a bit. If this happens, fine adjust your condenser polarizer to obtain complete extinction. Then fine adjust the rotatable analyzer to obtain an even darker field-of-view. Go back and fine adjust the polarizer again; and then the analyzer again. Repeat this a few times until you have obtained the most complete extinction, and then note the analyzer reading. The analyzer may not read “0,” although it should be close (the most I have seen these off is about 0.8°). Record this final analyzer angle as θ0; this will be a correction angle to be applied in the retardation equation:
In our case, you would subtract the small correction angle from your final analyzer rotation angle before multiplying by 3.033.
Discussion
The gray retardation colors are very difficult to determine accurately by visual estimate alone; I made an experiment to show this. Before I determined the retardation of the acrylic fiber above by Sénarmont compensation, I tried to estimate, to the best of my ability, the retardation color, by referring to a color Michel-Lévy chart, and its additional written description of the colors. The color temperature of the microscope illumination was 5500 Kelvin. I estimated the retardation to be 150 nm. I then sought out two additional experienced staff members, and asked each of them to estimate the retardation color. The first estimated 150 nm, as I had. The second, independently, also estimated 150 nm. However, the last staff member, knowing how difficult it is to estimate the grays accurately, inserted the first-order red compensator in both additive and subtractive positions, obtaining estimated values of 375 nm (2 o’clock – 8 o’clock) and 650 nm (10 o’clock – 4 o’clock). The idea here being that one can estimate colors other than gray more accurately than the grays themselves. 650 – 375 = 275. 275/2 = 137.5 nm. This staff member therefore changed his estimate from 150 nm to 137.5 nm. Then, noting that this was close to the value of an ordinary quarter-wave plate, predicted, confidently, that on insertion of the λ/4 compensator, essentially complete compensation would take place in the subtractive position. But it did not happen, because the retardation color was not 137.5 nm, nor was it 150 nm, as we had all estimated, but 57.0 nm, as determined by Sénarmont compensation. The fiber here was between 6 and 7 eyepiece divisions, or 16.25 µm in diameter. Our estimate of 150 nm for this acrylic fiber would yield a birefringence of 0.009 – too high. The 57.0 nm obtained through Sénarmont compensation results in a birefringence of 0.0035 – right on the money.
Figure 13 is the appearance of the fiber on inserting the green interference filter; and Figures 14, 15, and 16 represent the various rotations of the analyzer.
Conclusion
I like Sénarmont compensation because it is fast, easy, and inexpensive (at the time of this writing, Berek compensators are selling for $1,451.00; the Sénarmont compensator costs $297.00). It provides rapid, accurate determination of small relative retardations, which are perhaps more often encountered with biological samples than with industrial samples, but I use it with these also. Another class of samples I use it with is color-dyed synthetic fibers. The dyes mask the true retardation colors, and as I do not wish to alter such fibers by chemically removing the dye (they are usually of forensic interest), I use Sénarmont compensation to determine the retardation to obtain the birefringence.
According to Johannsen (2), it was Arago who discovered in 1811 that two mineral sections superimposed at right angles to each other show a reduction in the interference color, but Biot in 1813 who first suggested that the vibration directions in an unknown mineral could be determined by comparison with those of one which is known. Biot used a whole series of plates of different minerals of different thickness. If a mineral had the same optical character as the plate, he called it “attractive;” if opposite, “repulsive.” It was Sir David Brewster who, in 1818, gave to such minerals the names “positive” and “negative.” The use of thin plates of definite thicknesses was introduced by Airy in 1831, and H. de Sénarmont in 1851 first applied a half-wave plate to the determination of all three vibration axes.
Wright (4) refers to the Sénarmont method as the Sénarmont-Friedel method, because, as he reports in a footnote, de Sénarmont described his method in 1840, whereupon it seems to have been forgotten until the same method was described by G. Friedel in 1893. According to Johannsen, although Biot was the first to use a quartz wedge, de Sénarmont also later made use of it, “but subsequently seems to have been forgotten” until Sorby announced it as new in 1877.
It would appear that de Sénarmont’s methods of compensation are still being forgotten. I encourage you to try it if you have need, with your specimens, to determine small retardation values rapidly, accurately, and inexpensively. If you have the funds, the Berek is recommended.
References
1. The Michel-Lévy Interference Color Chart – Microscopy’s Magical Color Key. John Gustav Delly. (July 10, 2003).
2. Manual of Petrographic Methods. Albert Johannsen. McGraw-Hill, New York (1914, 1918; Hafner Facsimile of the 1918 Second edition, 1968).
3. Das Polarisationsmikroskop. E. Weinschenk. Herder & Co., Freibrug im Breisgau (1925).
4. The Methods of Petrographic-Microscopic Research. F.E. Wright. Carnegie Institution, Washington, D.C. (1911).
5. Crystals and the Polarizing Microscope. N. Hartshorne and A. Stuart. Edward Arnold, London. Fourth edition (1970).
6. The Spindle Stage: Principles and Practice. F. Donald Bloss. Cambridge University Press, Cambridge, London, New York (1981). Sénarmont compensation, pp. 265-272.
7. An Improved Sénarmont Retardation Analysis Method. R. G. Laughlin, et al. Journal of Microscopy 139, pp. 239-247 (1985).









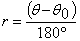





Comments
add comment